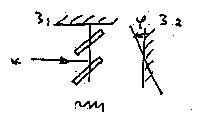
9.1(а). Что будет происходить с интерференционными полосами, наблюдаемыми в интерферометре Майкельсона, если одно из зеркал интерферометра отодвигать, оставляя параллельным самому себе, по ходу

падающего на него луча света?

Полосы сгущаются.

9.1(б).Как с помощью принципа Гюйгенса-Френеля можно обосновать с волновой точки зрения закон прямолинейного распространения света в однородной среде.

С помощью принципа Гюйгенса-Френеля удалось объяснить целый ряд дифракционных явлений, а также устранить одно из основных затруднений волновой теории света - показать, как согласуется волновая природа с наблюдающимся на опыте прямолинейным распространением света

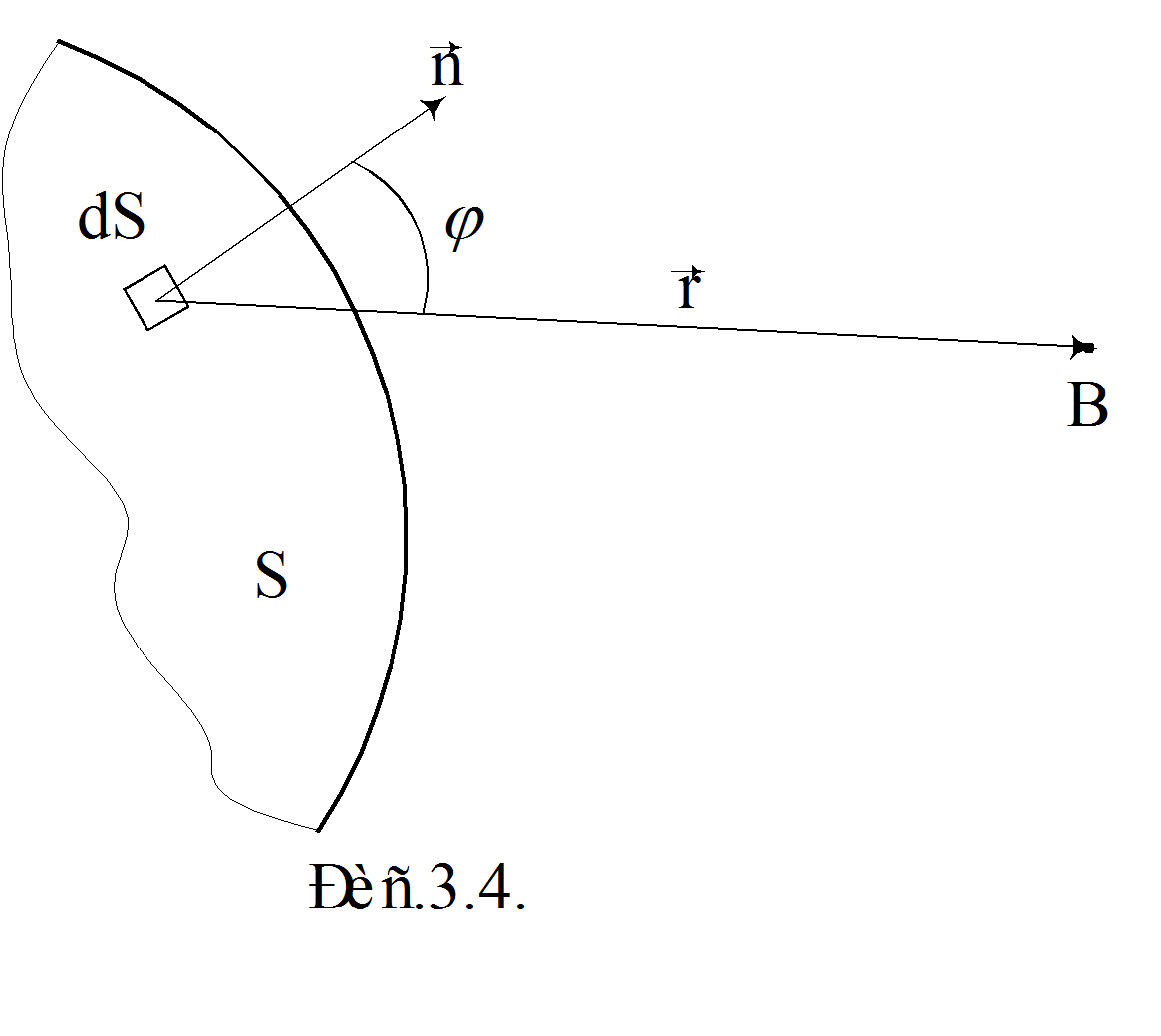
Согласно принципу Гюйгенса-Френеля каждый элемент dS волновой поверхности служит источником вторичной сферической волны, амплитуда которой удовлетворяет следующим условиям: она пропорциональна площади dS и убывает с расстоянием от источника по закону 1/r. От каждого участка dS волновой поверхности в точку наблюдения B (рис.3.4) приходит световое колебание

, (3.1)

где (t+₀) и E₀- фаза и амплитуда колебаний в месте, где расположен элемент dS, r - расстояние от элемента dS до точки B, k=2/ - волновое число. Коэффициент пропорциональности С() убывает при увеличении угла между нормалью к dS (вектором ) и вектором , причем С(0)=1, С(/2)=0.

Результирующее световое колебание в точке наблюдения представляет собой суперпозицию колебаний, дошедших в точку В от всех элементов поверхности S:

. (3.2)

Эта формула является аналитическим выражением принципа Гюйгенса-Френеля. Однако вычисления с использованием формулы (3.2) в общем случае чрезвычайно трудны и даже для простейших объектов (дифракция на круглом отверстии, прямоугольной щели) требуют использования нетривиальных численных методов.

9.1(в).Что такое эффект Керра? Какова физическая причина его возникновения?

Эффект Керра :1) электрооптический Керра эффект - возникновение двойного лучепреломления в оптически изотропных веществах (например, жидкостях и газах), помещенных в электрическое поле. Газ или жидкость в электрическом поле приобретают свойства одноосного кристалла с оптической осью вдоль поля. Эффект Керра объясняется различной по­ляризуемостью молекул жидкости по раз­ным направлениям. Это явление практиче­ски безинерционно, т. е. переход вещества из изотропного состояния в анизотропное при включении поля (и обратно) состав­ляет приблизительно 10^-10 с

2) Магнитооптический Керра эффект состоит в том, что плоско поляризованный свет, отражаясь от намагниченного ферромагнетика, становится эллиптически поляризованным.

Величина эффекта зависит от вещества, его температуры и длины волны света. В газах эффект Керра мал, а в жидкостях его величина гораздо больше. Аномально сильно он проявляется в нитробензоле и подобных ему жидкостях.\

9.1(г).Качественно нарисуйте зависимость интенсивности света от угла дифракции при падении параллельного пучка света на щель шириной D по углом 30 градусов к нормали (дифракция Фраунгофера Дифракция Фраунгофера - это дифракция на отверстии, которое для точки наблюдения открывает заметно меньше одной зоны Френеля. Это условие выполнено, если точка наблюдения и источник света находятся достаточно далеко от отверстия.

Дифракция Фраунгофера на одной щели Дифракция в параллельных лучах была рассмотрена Фраунгофером. Для получения пучка параллельных лучей света, падающих на щель или отверстие, обычно пользуются небольшим источником света, который помещается в фокусе собирающей линзы . П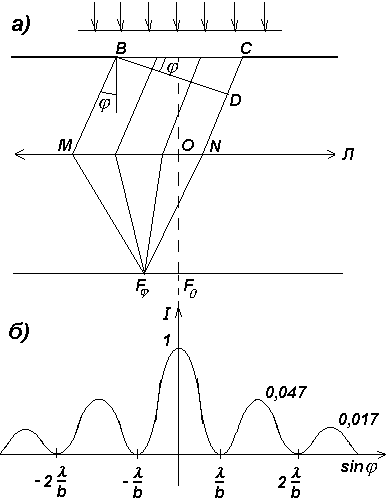усть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b (см. рис.4,а). Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом  к оптической оси линзы OF₀ =CD=bsin.

Разобьем щель ВС на зоны Френеля, имеющие вид полос, параллельных ребру В щели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от краев этих зон была равна /2.

При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами. Всего на ширине щели уместится :

/2= bsin/(/2) зон. Если число зон четное, т.е. bsin/( / 2)= 2m или bsin=m , m=1,2,3-, (8) то наблюдается дифракционный минимум (темная полоса). Если число зон нечетное, т.е. то наблюдается дифракционный максимум (светлая полоса). В направлении =0 наблюдается самый интенсивный центральный максимум нулевого порядка. Основная часть световой энергии сосредоточена в центральном максимуме. Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света . Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр.