Комплексное чило – число вида z=x+iy, где x действительная часть комплексно числа(ReZ), а y мнимая(ImZ)

Комплексное чило – число вида z=x+iy, где x действительная часть комплексно числа(ReZ), а y мнимая(ImZ)

Действия над кч

Сравнение a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).Сложение (a + bi) + (c + di) = (a + c) + (b + d)iВычитание (a + bi) − (c + di) = (a − c) + (b − d)i Умножение (a + bi)(c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i Деление

$\,\frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\,$

Тригонометрическая форма

Показательная форма

Корень н-ной степени из кч

Основные функции кп

- целая степенная функция f(z) = zⁿ, а так же корень и экспоненты.
- логарифмическая функция f(z) = Ln(z), Ln(z) = ln(|z|) + iarg z + 2kp i, k = 0, .1, .2,...
- тригонометрические функции

- гиперболические функции

ПРЕДЕЛ-Число A∈ℂ называют пределом функции f(z) комплексного переменного z в точке z₀∈ ℂ и обозначают

Непрерывность - Функция f(z) непрерывна в точке z₀, если

то есть если функция f(z) определена

в окрестности точки z0 и в ней самой, и

Дифференцируемость фкп в точке. Условия Коши-Римана.

Определение аналитической функции – функция, уоторая выполняет условия Коши-Римана в открытом подмножестве.

Условия Коши-Римана в полярных координатах

Гармони́ческая фу́нкция — вещественная функция $U$ , непрерывно дифференцируемая в евклидовом пространстве $D$ , удовлетворяющая уравнению Лапласа: $Δ U = 0$ , где $\Delta=\sum_{i=1}^n\frac{\partial^2}{\partial x_i^2}$ — сумма вторых производных по всем переменным.

Теорема 1.Если функция f(z) – регулярна в z, то ее действительная и мнимая части u = Re f (z) и

v = Im f (z) - функции гармонические. Т2.Если две функции u( x, y) и v( x, y) являются гармонически-сопряженными, т.е. _u = 0

и _v = 0 , и для этой пары выполнены условия Коши-Римана, то они определяют

регулярную функцию f(z) (с точностью до константы).

Геометрический смысл модуляи аргумента производной - |f’(z)|>1 – коэффициент растяжения <1- коэффициент сжатия …argf’(z) – угол между отображенными и первоначальными касательными к прямым

Конформное отображение - отображение одной фигуры (области) на другую, при котором две любые кривые, пересекающиеся под некоторым углом во внутренней точке первой фигуры, преобразуются в кривые второй фигуры, пересекающиеся под тем же углом.

Критерий конформности - w = f (z) конформно в z = ∞ , если функция w=f(1/z)=F(z) отображает

z = 0 конформно в плоскость W. w = f (z) отображает z = z₀ конформно в w = ∞ , если w=1/f(z) конформно отображает z = z₀ в w = 0

Линейная функция комплексного переменного - w = az + b (a,b∈ ℂ) . Эта функция осуществляет конформное отображение

расширенной комплексной плоскости (ℂ) на расширенную комплексную плоскость

Аналитичиность ее –

Степенная функция кп – w=zⁿ(n∈ N)

Аналитичность

W=zⁿ является однолистной в угле раствора 2Pi/n

w = zⁿ конформно отображает угол раствора

2π/n на плоскость с разрезом.

Показательная функция –

W=e^z

Аналитичность –

Областью однолистности является полоса M = {z∈ ℂ:b < Imz < b + 2π } , которая отображается на всю плоскость с разрезом по лучу θ = b

Функция z w = e осуществляет отображение ℂ→w→ℂ \ {0} , которое является

однозначным, но не взаимнооднозначным.

Lnz Так как функция w = ln z - многозначная, то рассмотрим отображение,

осуществляемое его главным значением, т.е. функцией ln z . Эта функция обратная по

отношению к z e , конформно отображает плоскость с разрезом (−∞,0] на полосу шириной

2π , параллельную действительной оси

Определение интеграла от функции комплексного переменного - Если существует и он не

зависит от способа разбиения

и выбора точек k M , то он называется интегралом f(z) по дуге AB и

обозначается

его связь с криволинейными интегралами –

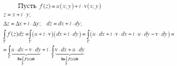
- криволинейный интегралы 2 рода

Интегральная теорема Коши для односвязной области- Если f(z) – регулярна в D, а D – односвязна, то интеграл по

любому замкнутому контуру γ лежащей D равен нулю:

Интегральная теорема Коши для многосвязной области Если f(z) – регулярна в области D, ограниченной кривыми: то - полная граница области

Интеграл от аналитической функции, его независимость от пути интегрирования

Формула Н-Л

Интегральная формула Коши для аналитической функции

Бесконечная дифференцируемость аналитических функций. Интегральная формула Коши для производных аналитической функции. Функция f(z) – регулярна в замкнутой односвязной области D

(в том числе в точке z₀ ), следовательно, существуют производные всех порядков в z₀ и

Степенной ряд - где n C и 0 z -

комплексные числа, а z - комплексная переменная.

Теорема Абеля- Во всех точках z внутри круга сходимости степенной ряд абсолютно

сходится и его сумма

Для любого степенного ряда существует круг с центром в точке z₀ , внутри

которого степенной ряд абсолютно сходится, а вне его – расходится.

этот круг называется кругом сходимости, а его радиус R -

радиусом сходимости.

Разложение аналитической в круге функции в ряд Тейлора. Формулы для коэффициентов. - Функция f (z) , регулярная в круге раскладывается в ряд по степеням Этот ряд называется рядом Тейлора. - коэффициент – формула

Ряд Лорана. Разложение функции, аналитической в кольце, в ряд Лорана. - Функция f (z) , регулярная в кольце раскладывается в ряд по степеням где Этот ряд называется рядом Лорана. Его можно представить в виде суммы двух рядов: Первое слагаемое этой суммы называется главной частью ряда Лорана, а второе – правильной частью.

Изолированные особые точки однозначного характера и их классификация. Точка z₀ называется изолированной особой точкой функции f (z) , если f (z) регулярна в некоторой окрестности точки z₀ за исключением самой этой точки. Точка z₀ - устранимая особая точка, если в разложении функции f (z) в ряд

Лорана в ее окрестности отсутствует главная часть, т.е. Особая точка z₀ функции f (z) называется существенной особенностью, если главная часть ряда Лорана содержит бесконечное число слагаемых.

Определение ряда Лорана в окрестности конечной особой точки и в окрестности бесконечно удаленной точки – бесконечно уд.т. (не содержит положительных степеней)

(конечное число слагаемых с положительными степенями z)

- (бесконечное число слагаемых с положительными степенями)

в окрестности изолированной особой точки.

Нули аналитической функции. Связь между порядком нуля и порядком полюса - Точка z₀ называется нулем n-го порядка регулярной функции f (z) , если

Если f (z) регулярна и имеет в z₀ нуль порядка m , то 1/f(z) имеет в этой точке z₀ полюс m -го порядка.

Определение вычета функции в конечной точке. Вычисление вычета в простом и кратном полюсе. Определение вычета функции в бесконечно удаленной точке. - - вычет функции f(z) в точке z₀

Вычеты фунцкции в простом полюсе

- в кратном полюсе

Если z₀ - существенно особая точка, то вычет вычисляется только как C₋₁

Первая теорема о вычетах - Пусть f (z) регулярна в конечной односвязной области D за исключением конечного числа изолированных особых точек замкнутая кривая, лежащая в D и содержащая Тогда:

Вторая теорема о вычетах - Пусть f (z) регулярна в расширенной комплексной плоскости ℂ за исключениемконечного числа изолированных особых точек, считая точку z = ∞ . Тогда:

Приложение теории вычетов к вычислению несобственных интегралов от рациональных функций

степень числителя должна быть по крайней мере на 2 меньше степени знаменателя

Лемма Жордана. Вычисление несобственных интегралов вида , где - правильная рациональная дробь,

f(z) – регулярна в верхней полуплоскости полуокружность радиуса R с центром в точке

z = 0 , лежащая в верхней полуплоскости.

Теорема о логарифмическом вычете - Если f(z) регулярна в за исключением конечного числа полюсов и

Принцип аргумента - где приращение аргумента при обходе точкой z контура Г один раз в положительном направлении.

Теорема Руше - Пусть f(z) и g(z) регулярны в ограниченной односвязной области D и на ее границе Г_D и пусть Тогда f(z) и F(z) = g(z) + f (z) имеют в D одинаковое число нулей.

Определение Гамма-функции как несобственного интеграла. Область сходимости соответствующего интеграла. Свойства Гамма-функции: формула понижения, формула дополнения. - Интеграл сходится для любого x > 0 . Формула привидения - формула дополнения -

Производная от Гамма-функции и область сходимости соответствующего ей несобственного интеграла. гаммма функция бесконечно дифференцируема при любом

Бета-функция. Определение и основные свойства. Применение к вычислению интегралов. - Интеграл сходится при любых x > 0, y > 0 . Свойства - , , Приминение к вычеслению интегралов заключается в сведении интегралла к виду B функции, замены на Г функцию и при возможности вычисления значений Г функций.